P1004 [NOIP 2000 上級組] 格子での数の取得

問題背景

NOIP 2000 上級組 T4

問題文

\(N \times N\) の格子図 \((N \le 9)\) があり、そのいくつかのマスには正の整数が書かれ、他のマスには数字 \(0\) が入っています。下図のようになります（サンプル参照）:

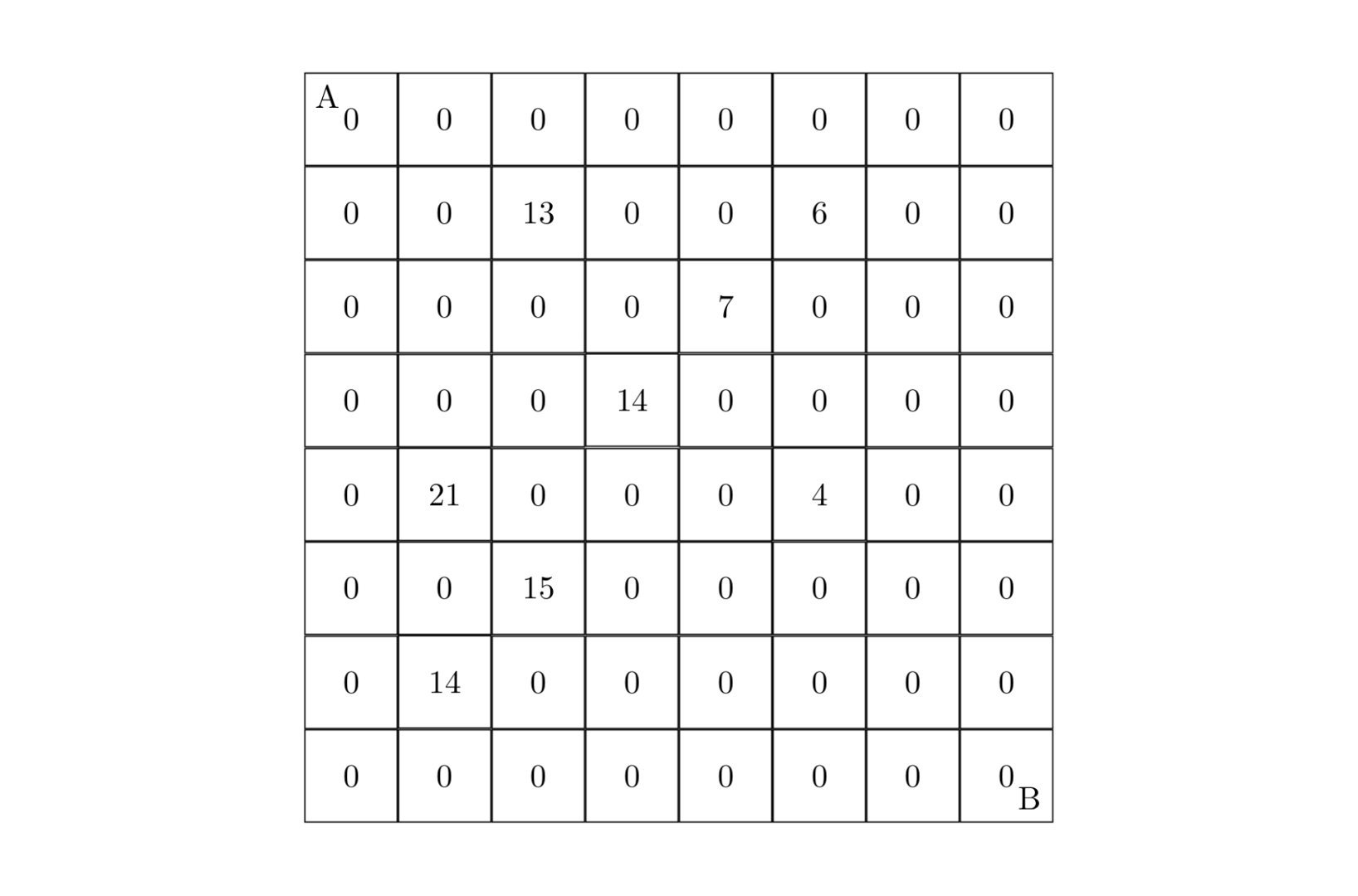
ある人が左上の点 \(A\) から出発し、右または下に移動しながら右下の点 \(B\) に到達します。通ったマスの数値を取得できます（取得後、そのマスは \(0\) になります）。
この人は \(A\) から \(B\) まで \(2\) 回 移動します。取得できる数の合計が最大となるように、\(2\) 本の経路を求めてください。

入力形式

最初の行には整数 \(N\) が与えられます（\(N \times N\) の格子のサイズ）。
次の各行には \(3\) つの整数があり、最初の \(2\) つは位置を表し、最後の \(1\) つはその位置に置かれる数です。
単独の \(0\) だけが書かれた行で入力が終了します。

出力形式

整数を \(1\) つ出力してください。それは \(2\) 本の経路で取得できる数の合計の最大値です。

入出力例 #1

入力 #1出力 #1

8
2 3 13
2 6  6
3 5  7
4 4 14
5 2 21
5 6  4
6 3 15
7 2 14
0 0  0

67

説明／ヒント

データ範囲: \(1 \le N \le 9\)。