P1002 [NOIP 2002 初級組] 川渡りの兵士
問題文
チェス盤の上に、\(A\) 点に兵士がいて、目標地点 \(B\) に到達する必要があります。
兵士の移動規則は「下に移動する」または「右に移動する」です。
同時に、盤上の \(C\) 点に相手のナイトがいます。
ナイトが立っているマスと、ナイトが \(1\) 回のジャンプで到達できるすべてのマスを「ナイトの制御点」と呼びます。
したがって、この問題は「ナイトが川渡りの兵士を妨害する」と呼ばれます。
チェス盤は座標で表されます:\(A\) 点は \((0, 0)\)、\(B\) 点は \((n, m)\) にあり、ナイトの座標が入力として与えられます。
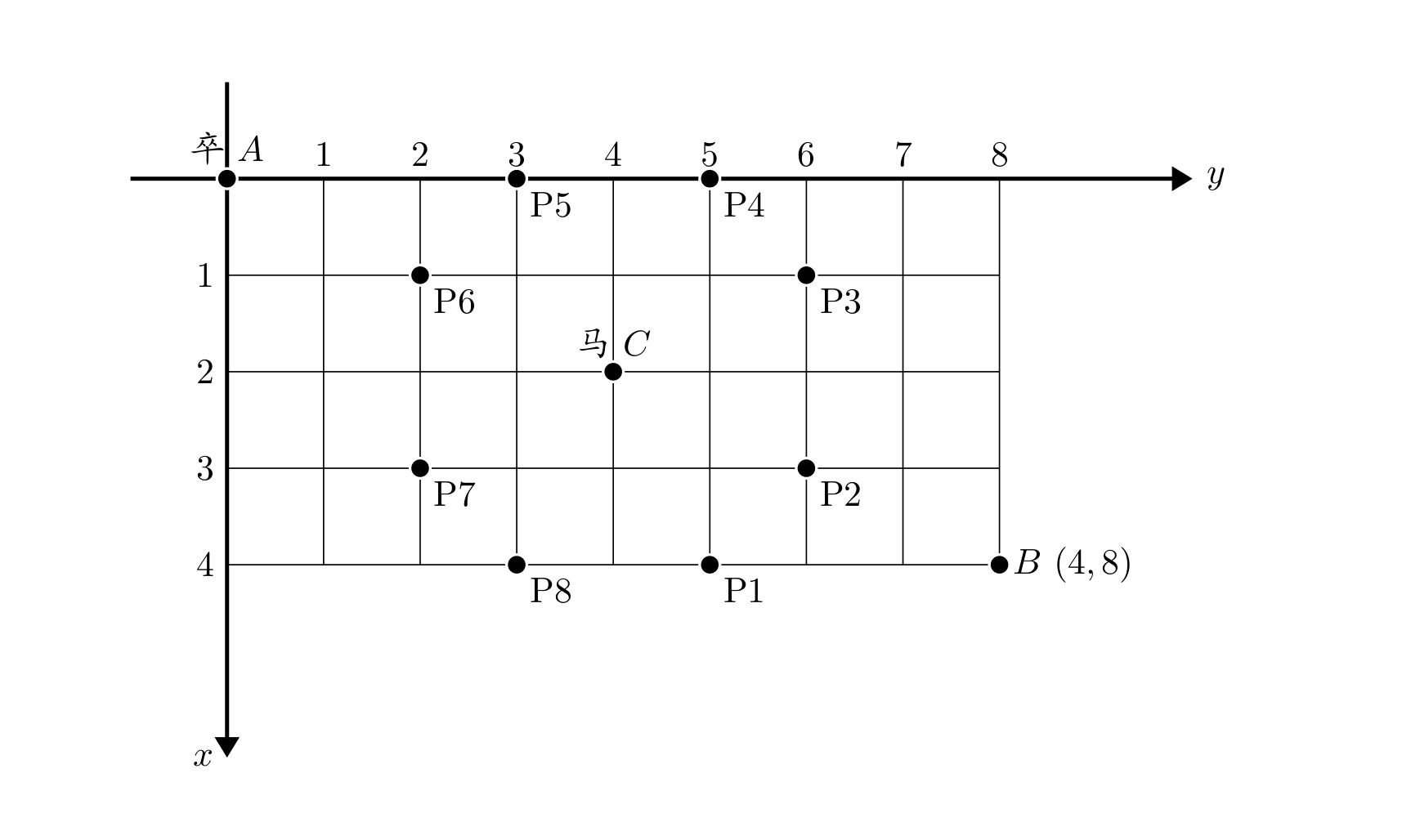
ナイトが固定された位置に留まり、兵士と一緒に動かないと仮定して、\(A\) から \(B\) まで兵士が到達する経路の総数を求めてください。
入力形式
\(B\) の座標とナイトの座標を表す \(4\) つの正の整数が \(1\) 行で与えられる。
出力形式
経路の総数を表す \(1\) つの整数を出力せよ。
入出力例 #1
説明/ヒント
データの \(100\%\) に対して、\(1 \le n, m \le 20\), \(0 \le\) ナイトの座標 \(\le 20\) が成り立つ。
【出典】
NOIP 2002 初級組 第 \(4\) 問