Skip to content

P1003 [NOIP 2011 Advanced Group] Carpet Laying

Description

To prepare for a unique award ceremony, the organizers are laying rectangular carpets on a rectangular area of the venue (which can be regarded as the first quadrant of a Cartesian coordinate plane). There are \(n\) carpets in total, numbered from \(1\) to \(n\). The carpets are laid in order of increasing number, parallel to the coordinate axes. Later carpets cover earlier ones.

After all carpets are laid, the organizers want to know which carpet is on top at a given point of the ground. Note: points on the carpet boundary and vertices are also considered covered.

Input

The input consists of \(n+2\) lines.

The first line contains an integer \(n\), the total number of carpets.

The following \(n\) lines describe the carpets. The \((i+1)\)-th line contains four integers \(a, b, g, k\), separated by spaces, representing the lower-left corner coordinate \((a, b)\) and the lengths of the carpet along the \(x\)-axis and \(y\)-axis.

The last line contains two integers \(x, y\), representing the coordinates \((x, y)\) of the point of interest.

Output

Output one line containing a single integer: the number of the carpet covering \((x, y)\). If the point is not covered by any carpet, output -1.

Sample #1

3
1 0 2 3
0 2 3 3
2 1 3 3
2 2

3

Sample #2

3
1 0 2 3
0 2 3 3
2 1 3 3
4 5

-1

Note / Hint

Sample #1 Explanation

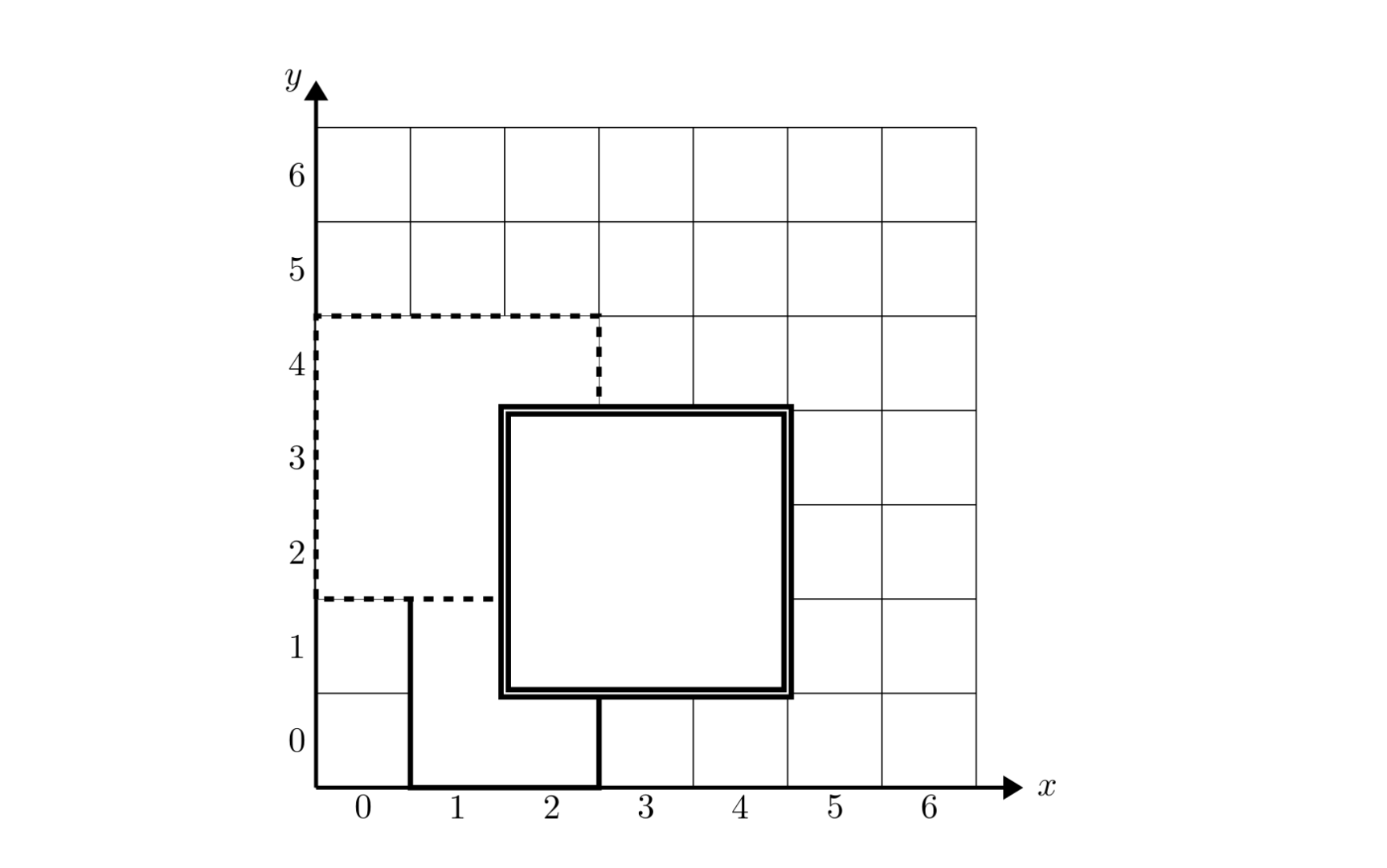
In the figure below, carpet \(1\) is shown with solid lines, carpet \(2\) with dashed lines, and carpet \(3\) with double solid lines. The topmost carpet covering point \((2,2)\) is carpet \(3\).

Data Range

  • For \(30\%\) of the data, \(n \le 2\).
  • For \(50\%\) of the data, \(0 \le a, b, g, k \le 100\).
  • For \(100\%\) of the data, \(0 \le n \le 10^4\), \(0 \le a, b, g, k \le 10^5\).

NOIP 2011 Advanced Group Day \(1\), Problem \(1\).