P1002 [NOIP 2002 Beginner Group] River-crossing Soldier
Description
On the chessboard, there is a soldier at point \(A\) that needs to reach the target point \(B\).
The soldier's movement rules: it can move down or to the right.
At the same time, there is an opponent's knight at point \(C\) on the board.
The square where the knight stands and all squares that can be reached by a single knight jump are called the knight's control points.
Therefore, this problem is called "Knight blocking the crossing soldier."
The chessboard is represented by coordinates: point \(A\) is at \((0, 0)\), point \(B\) is at \((n, m)\), and the coordinates of the knight are given as input.
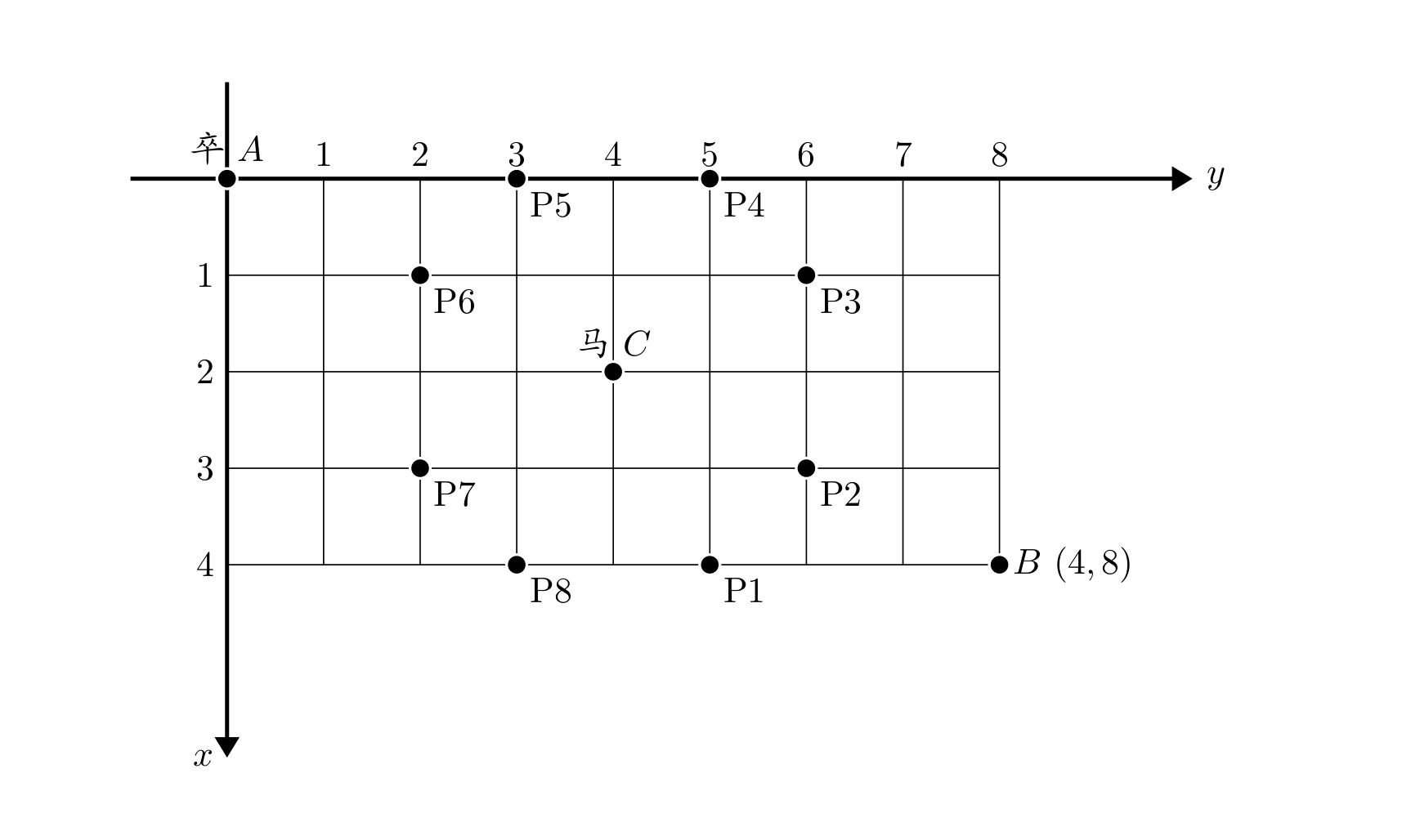
You are asked to calculate the number of paths for the soldier to reach point \(B\) from point \(A\), assuming the knight stays in a fixed position and does not move with the soldier.
Input
One line with four positive integers, representing the coordinates of point \(B\) and the knight.
Output
One integer, representing the total number of paths.
Sample #1
Note / Hint
For \(100\%\) of the data, \(1 \le n, m \le 20\), \(0 \le\) knight coordinates \(\le 20\).
[Problem Source]
NOIP 2002 Beginner Group, Problem \(4\)